NIM is a simple but potentially infuriating, ancient 2 player game. You have some counters or matchsticks, you’re allowed to take a limited number in each turn, say 1, 2 or 3. The winner is the person who takes the last counter.
Sometimes it’s played the other way round, so the player left with the last counter loses. This is called a misère game, but there’s enough misère in the world as it is, frankly, so we’ll play the happier version of the game today.
Thinking about this game makes a great maths investigation, and it can be a good computing activity too. Challenge your students to write a program that will play and beat a human, or modify and improve the programs I’m going to show you in this video.
As you can learn a simple trick to always win NIM, it also makes a great game to annoy people with, as Matt Parker of Stand Up Maths shows in his superb video about the game and a 60s American plastic computer version of it. Watch his video, just as soon as you’ve finished watching this. He and his colleagues also played this game with members of the public on the South Bank in London, using pegs and trying to get people to win £20 off them, which they could never do.
The wonderful folk at the NRICH project at the University of Cambridge have written up a lovely simple version here: https://nrich.maths.org/1204
I used to use NRICH games and resources a lot when I was teaching primary school maths, I highly recommend them for creative maths investigations.
Back in the 1970s there was even a version of NIM for the Sinclair Cambridge Programmable calculator. You can read a bit about that elsewhere on my blog.
Anyway, I decided to see if I could write a BBC micro:bit program so that the micro:bit could play a human at NIM and always win. Perhaps you could challenge your students to do the same and see what they come up with – can they identify winning strategies, and abstract them into a working computer program?
I approached this challenge by taking the really simple NRICH example and applying Matt Parker’s strategy from his Dr Nim video.
The key here is to think of the end game and the position you want to get your opponent into.
In the Dr Nim game Matt Parker shows in his video, you have 12 marbles and can take 1, 2 or 3 counters in each turn. So he chunks the game into multiples of 4.
In every go, whatever you take, Dr Nim will take whatever number he needs to make sure you’ve taken 4 between you.
oooo / oooo / oooo
So if you take 1
oooo / oooo / ooo
Dr Nim will take 3.
oooo / oooo /
If you take 2
oooo / oo
he’ll take 2.
oooo /
If you take 3,
o
he’ll take 1 – and win!
Now, we’re computer scientists so we always want to abstract some kind of pattern if we can, to make any coding more efficient, so straight away I notice that if the human takes n counters, Dr Nim takes 4-n counters.
Also I notice that with the option to take up to x counters, you want to break down into chunks of x+1, so that if your opponent goes first, you always have the advantage. You want to make sure they always have x+1 counters at some point when it’s their turn to go.
Hold that thought! We’ll come back to it later.
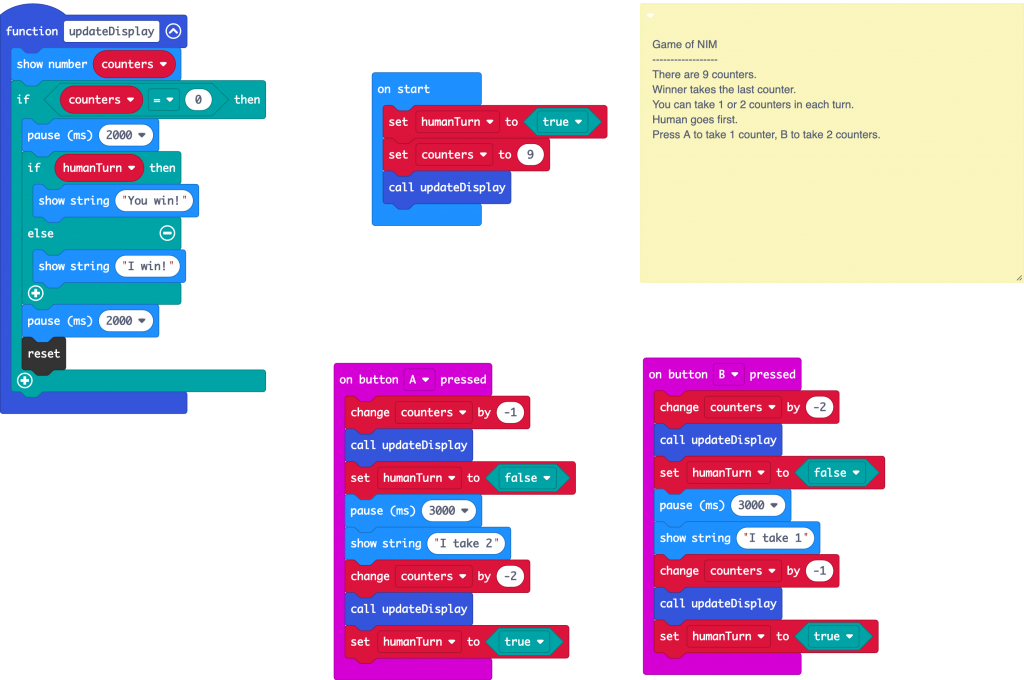
So, back to our micro:bit version of the game. I’m going to follow the NRICH example and say you can only take 1 or 2 counters in each turn, but I’m going to start with 9 counters instead of 7.
This simple version is easier to think about, work out all the permutations, and easier to code. Also we can use micro:bit button A to take 1 counter, and button B to take 2 counters, so we’ve got a nice simple user interface.
So I coded a version for the micro:bit. Try and beat it:
You could play many more games, and trust me the micro:bit will always win.
So how does it work?
Remember Matt Parker with his 12 marbles or pegs which he treated as 3 lots of 4? Well he had sets of 4 because the choices were to take 1, 2 or 3. The chunk you’re working with should be one more than the highest number you can take in a turn.
We can only take 1 or 2 counters in our micro:bit version of the game, so we’ll treat it as three lots of three:
ooo / ooo / ooo
We’ll make the sap, sorry the human, go first. Remember, in a pair of turns, we need to make sure the human and machine have taken 3 counters between them.
Each time, if the human takes 1 counter…
ooo / ooo / oo
our program will take 2:
ooo / ooo /
If they take 2
ooo / o
the program will take 1:
ooo /
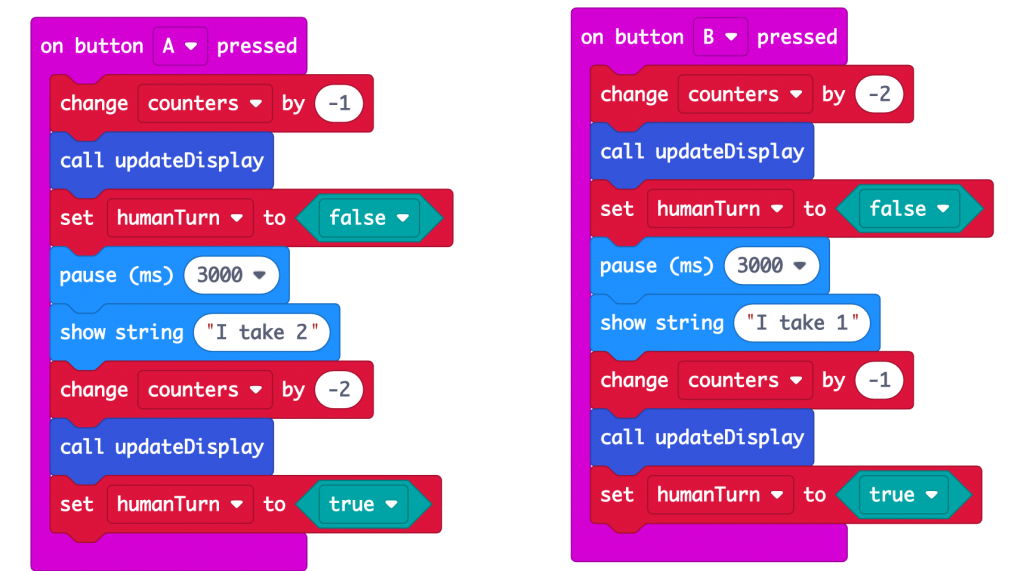
As there are only two choices at each turn, we can hard code this into blocks that follow each button press:
Here we use a function to update the display and check if the game’s over. I added a bit of logic to show different messages depending on whose turn it was when the last counter was taken, though with these numbers, the ‘you win!’ message will never be displayed. Try altering the number of counters you start with and see if that makes a difference. Does the program still work?
Now, do you notice anything about these two sets of code?
They are very similar! There’s a pattern here, and when computer scientists spot patterns, they get all excited because there’s an opportunity to be clever and make the code more compact.
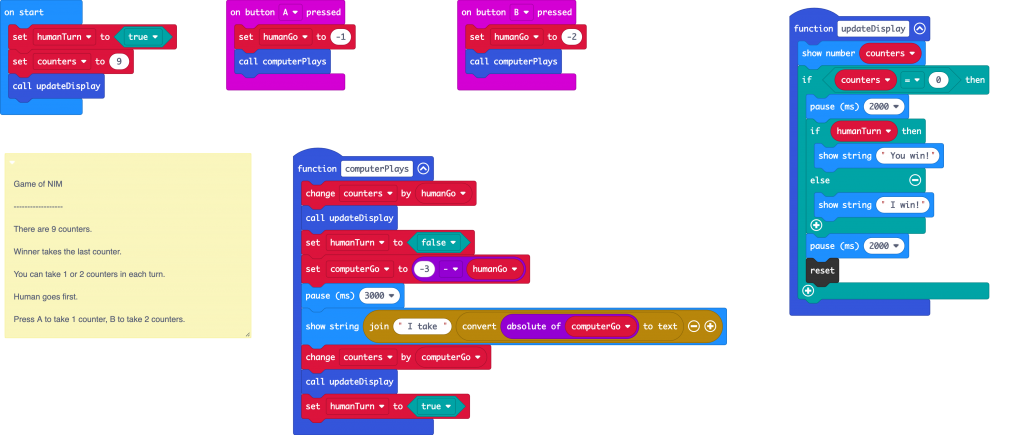
We do that in this new version of the project by creating a function that does the same work, just slightly differently depending on how many counters the human took.
Remember that formula 4-n earlier? I spotted that in Dr Nim, if the human takes n or marbles, Dr Nim would always take 4-n marbles and be guaranteed to win, because that game works in blocks of 4 counters.
I kind of use that here.
The variable humanGo keeps track of how many counters the human player took.
We set the number for the computer to take, by using 3-n. Our game works in blocks of 3, so we set the computer’s go to be 3 (or minus 3 here) minus the human go.
Why is it minus 3 here not 3? I’m using negative numbers here just to make the block simpler when we change the total number of counters, stored in the counters variable. MakeCode doesn’t have a block to change the sign of a number. Well, not yet. I’ll have to see what I can do about that. I’ve managed to sneak at least one new block into MakeCode, possibly even one used in this project, it’d be fun to have another one to call my own.
So this version of the code works in exactly the same way, it’s just a bit more efficiently coded. It’s cleverer, using a function to avoid repeating two very similar sets of code.
But is it easier to read, follow and understand?
Probably not. This is something that would make a great discussion point with a class of students. Which version of these programs is ‘better’? Which is easier for someone to come along and understand and modify, or if you yourself look back at your own code months or years later and wonder how on earth you wrote it and what it does?
The first one makes it very easy to follow what happens in each case. But if you want to adapt this to play a more complex version of NIM, say with 12 counters and the ability to take 1, 2 or 3 at each turn, the version with the clever function is probably going to be more adaptable.
Have a play with these, and if you adapt my code to make a more advanced game of NIM, please let me know. You could use shake gestures, wire up 3 tin foil buttons to the pins, or use the touch logo on the new micro:bit (V2) to get more button inputs for more choices.
Like the Dr Nim game in Matt Parker’s video, perhaps you can create an ‘equaliser’ mode where the poor human player has at least a chance of winning?
Have fun annoying your friends and relations with your unbeatable NIM micro:bit machines!
Oh, and here’s that Matt Parker video on Dr Nim: