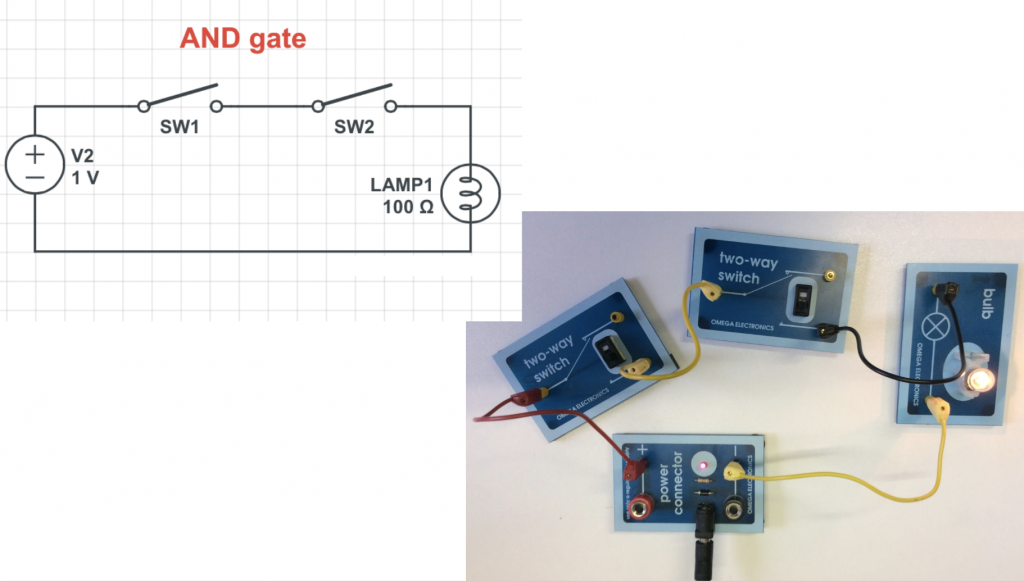
I found teaching logic gates one of the trickier parts of the secondary Computer Science curriculum: they’re abstract, dry… not much fun. Year 9 in a girls’ school. Tough crowd. To counter this, I tried to make them a bit more tangible. I raided the Physics (or was it DT?) department for these rather splendid, and tragically no longer manufactured, modular lightbulbs and switches to make AND and OR gates we could wire up in class:
You can make a NOT gate with a relay, but beyond that it gets tricker. There are modular logic gates you can buy, but they’re very expensive, so I switched to using the marvellous logic.ly website to get my pupils to wire logic gates together to make half adders and full adders – the building blocks of everything from calculators to phones to computers. With my year 9s, logic gates made more sense when we could use them to add up:
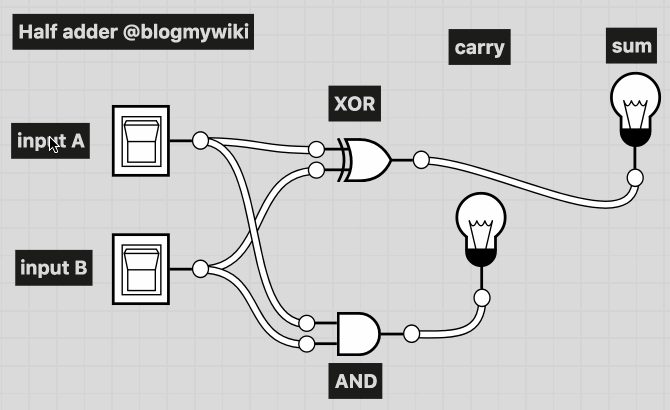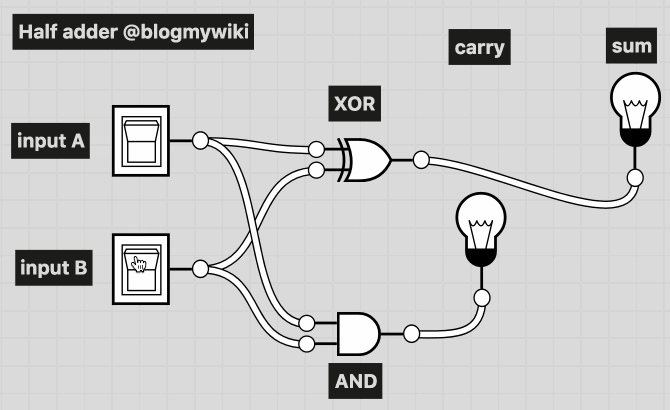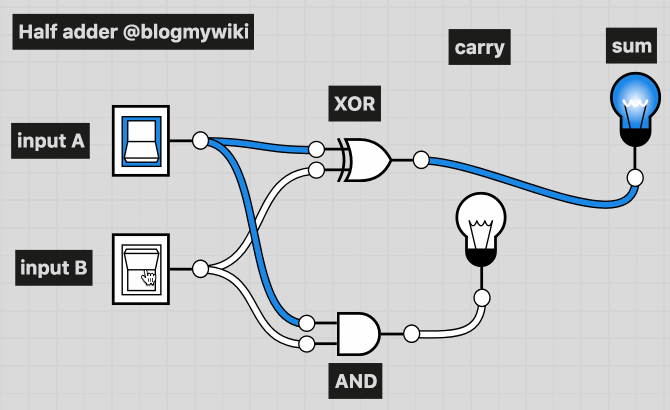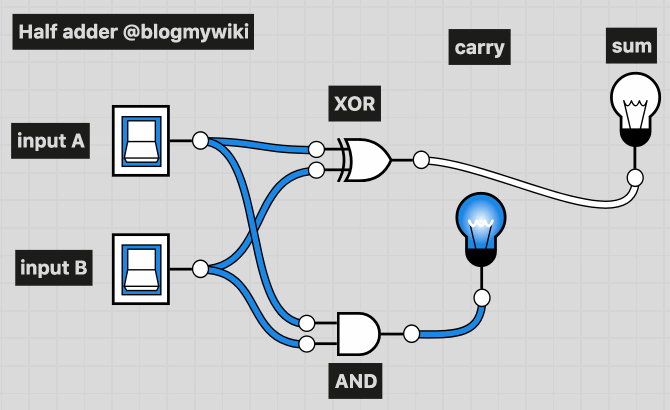
Here you can see two switches used as inputs to the half adder. The lightbulbs show the output. With both switches off (0 + 0) you get no lights: 00 in binary. With either input switch on (1 + 0 or 0 + 1) you get 01 binary out. Turn both switches on, however, 1 + 1 = 10, which in binary is true as 10 is how you write the number 2 in binary.
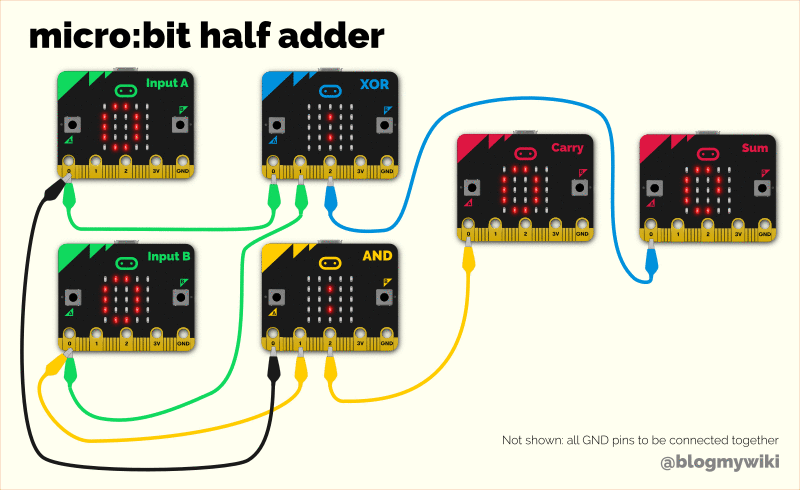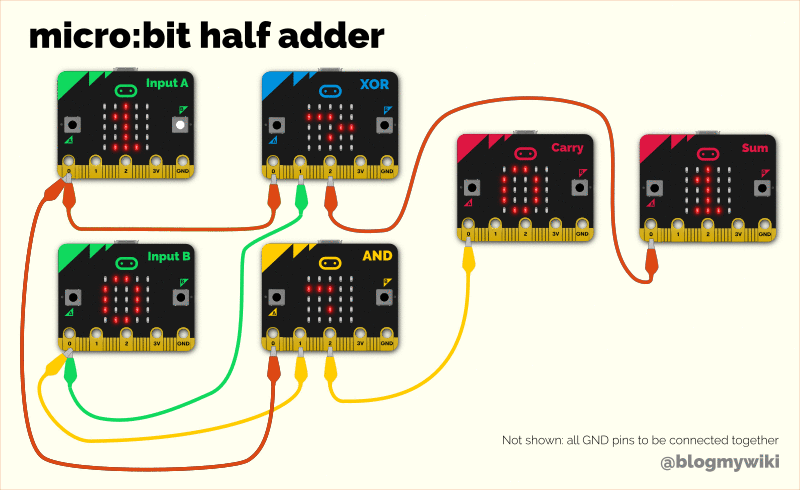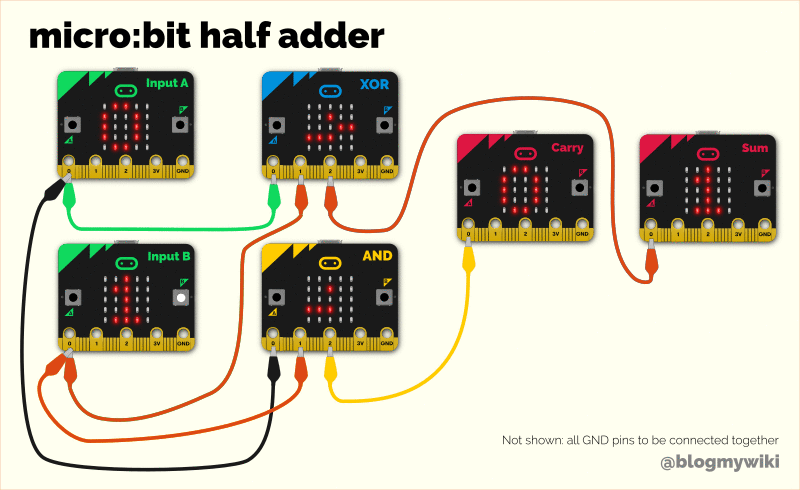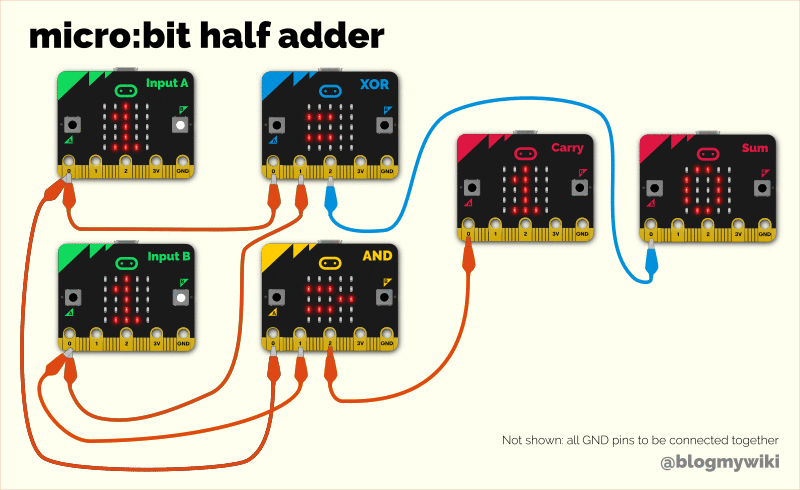
More recently I made some simple MakeCode programs to turn micro:bits into physical logic gates so you can make a half adder. You’ll need 6 micro:bits and a heap of crocodile clip or banana plug leads for this, plus battery packs – though you could get pairs of pupils to program each element, or write the programs themselves from scratch.
There are 4 kinds of device:
input switches which send a digital output 0 or 1. Press button A for 0, button B for 1, which sends a digital 1 from the pin 0 output.
AND gates send a digital 1 output on pin 2 if input pins 0 and 1 are high,
XOR gates send an output on pin 2 if either inputs on pins 0 or 1 are high, but not both.
output displays show 0 or 1 depending on whether they receive a digital input on pin 0.
You do also have to join all the GND pins together to complete the electrical circuit, certainly if you’re using batteries – you can daisy chain them together. I didn’t show that on the diagram above for clarity. (If you’re powering them all off the same USB supply you may get away without daisy-chaining the GND pins together for reasons not unadjacent to witchcraft).
Here’s the code for the input switch:
The XOR gate:
The AND gate:
The output display:
…and here’s a video showing them in use, albeit messily on my desk:
And yes, the irony of using a micro:bit – which contains thousands and thousands of logic gates – to emulate a single logic gate is not lost on me. But you may have a class set of micro:bits that could help make logic gates more tangible. You could make other logic gates to get a full set. Could you build a full adder? A bigger calculator? Something else?